7003全讯入口在拓扑量子计算研究方面取得重要进展
来源： 供稿： 摄影： 审核：陈珂 作者： 发布时间：2023-09-15 浏览量：
日前，7003全讯入口7003全讯入口张向东教授课题组利用经典电路平台，实验展示了拓扑量子计算有关的编织以及算法等功能。相关成果以“Experimental Simulation of Topological Quantum Computing with Classical Circuits”为题发表在Advanced Intelligent Systems期刊[Advanced Intelligent Systems, 2023, 2300354]上，详细内容也可参考 arXiv:2309.04896 。该工作得到了国家重点研发计划以及国家自然科学基金委的大力支持。7003全讯入口集成电路学院博士后邹德源、7003全讯入口博士生潘乃桥和陈天副教授为该论文的共同第一作者，7003全讯入口7003全讯入口张向东教授、陈天副教授，信息与电子学院孙厚军教授为论文共同通讯作者。
研究背景
量子计算在诸多方面，如质因数分解、搜索算法以及模拟真实物理系统等， 已被证明有优于经典计算机的强大计算能力，近些年受到了人们极大关注。但是，由于量子态非常易于受环境干扰产生退相干和量子操作精度有限导致差错, 以至于实现通用量子计算机非常困难。而适用于特定量子算法的量子模拟机，也因为受到量子退相干的影响，目前依然处于实验室演示阶段。
拓扑量子计算机的提出则为实现稳定的量子计算、甚至通用量子计算提供了一个新的途径。其中一类拓扑量子计算机的实现是依赖于具有非局域特性的马约拉纳零能模式。由于这样的马约拉纳零能模受到粒子空穴对称性保护，因而在局域扰动中能保持鲁棒特性。在2001年，A. Y. Kitaev (Phys.-Usp. 44 131 (2001)) 预言在一维拓扑超导体的两端存在马约拉纳零能模。同年，D. A. Ivanov (PRL, 86, 268 (2001)) 提出使用这样的零能模进行编织操作，可以实现普适量子计算所需要的一系列单比特门和两比特控制门。因而，如果能够实现马约拉纳零能模、并且操控零能模进行特定的编织，就可以展示拓扑量子计算的功能。J. Alicea等人 (Nat. Phys. 7, 412 (2011)) 在理论上提出利用s波超导体和半导体纳米线可以制备出马约拉纳零能模，并且使用T型结构演示了零能模的编织。然而由于这样的理论方案在实验实现上非常困难，甚至在实验中能否产生马约拉纳零能模都引起了极大争论。特别是最近几年Nature和Science的撤稿事件，人们对能否实现拓扑量子计算都产生了质疑。在时隔16年Science再次发布的“全世界最前沿125个科学问题”中，“Can topological quantum computing be realized?”（拓扑量子计算可以实现吗？）被列入其中 （见Information Science（信息科学）中第3个问题）。
在本工作中，研究人员克服了前期理论方案难以实验实现的一些困难，设计出了新的电路系统，实验上证明了拓扑量子计算是可以实现的。具体的，研究人员在实验中利用经典电路构造出具有拓扑保护的类马约拉纳零能模，并通过操控这些零能模实现了编织；进一步，通过激发多个零能模演示了单比特门和两比特门；最后，使用多步编织展示了Grover搜索算法。
研究亮点之一：基于经典电路构造出具有拓扑保护的类马约拉纳零能模并展现其编织功能
研究人员首先在经典电路上通过设计电路节点的连接，展示了在电路两端有粒子-空穴对称性的类马约拉纳零能模，并且验证了鲁棒性。研究人员通过调节电路中电阻和电容的大小，来有效模拟不同节点间的耦合强度。具体电路结构如图1（a）所示，图中显示了对应于Kitaev模型中两个原胞的电路，每个原胞包含四个电路节点（A-D）。该电路的优点是只需要考虑不同电路节点之间的连接关系，而不需要考虑它们的位置。图中的蓝线和红线表示两个原胞之间节点的连接，详细的连接模式如图1（b）所示。图1（b）中的蓝色和红色箭头表示负阻抗转换器，这种器件基于电流方向会具有不同的阻值，它们的结构如图1（c）中的蓝框和红框所示。图1（a）中的绿色箭头表示原胞内耦合，具体结构如图1（c）的绿色框所示。图1（a）中绿线上的红点和蓝点是可以确定链接是否存在的开关，具体结构显示在图1（c）的黑框中。
基于上述电路模型，研究人员可以在电路系统中研究Kitaev模型中的类马约拉纳边缘态。通过控制绿线上的开关来产生具有拓扑或平庸相位的电路段。对于具有拓扑和平庸相的电路网络，通过向网络输入外部电源，平庸段和拓扑段之间的边界处则会出现拓扑边缘态。这时如果改变边界处原胞中的绿线开关，拓扑边缘态就会被转移到相邻原胞。这意味着可以沿着电路网络自由地移动拓扑边缘态。
实验中研究人员展示了一个具有10个原胞的电路网络，这些原胞被标记为从1到10，如图1（d）和1（e）所示。在3到8中的所有原胞都为拓扑相，而1到2，以及9到10的单元都为平庸相。当接入外部电源时，电压分布的模拟结果和实验结果分别显示在图1（d）和1（e）中。可以清楚地看到，在拓扑段（原胞3和8）的边缘出现了一对拓扑边缘态。通过比较，研究人员发现实验和模拟结果基本相同。它们之间的差异来自于电路的损耗和元件的误差。
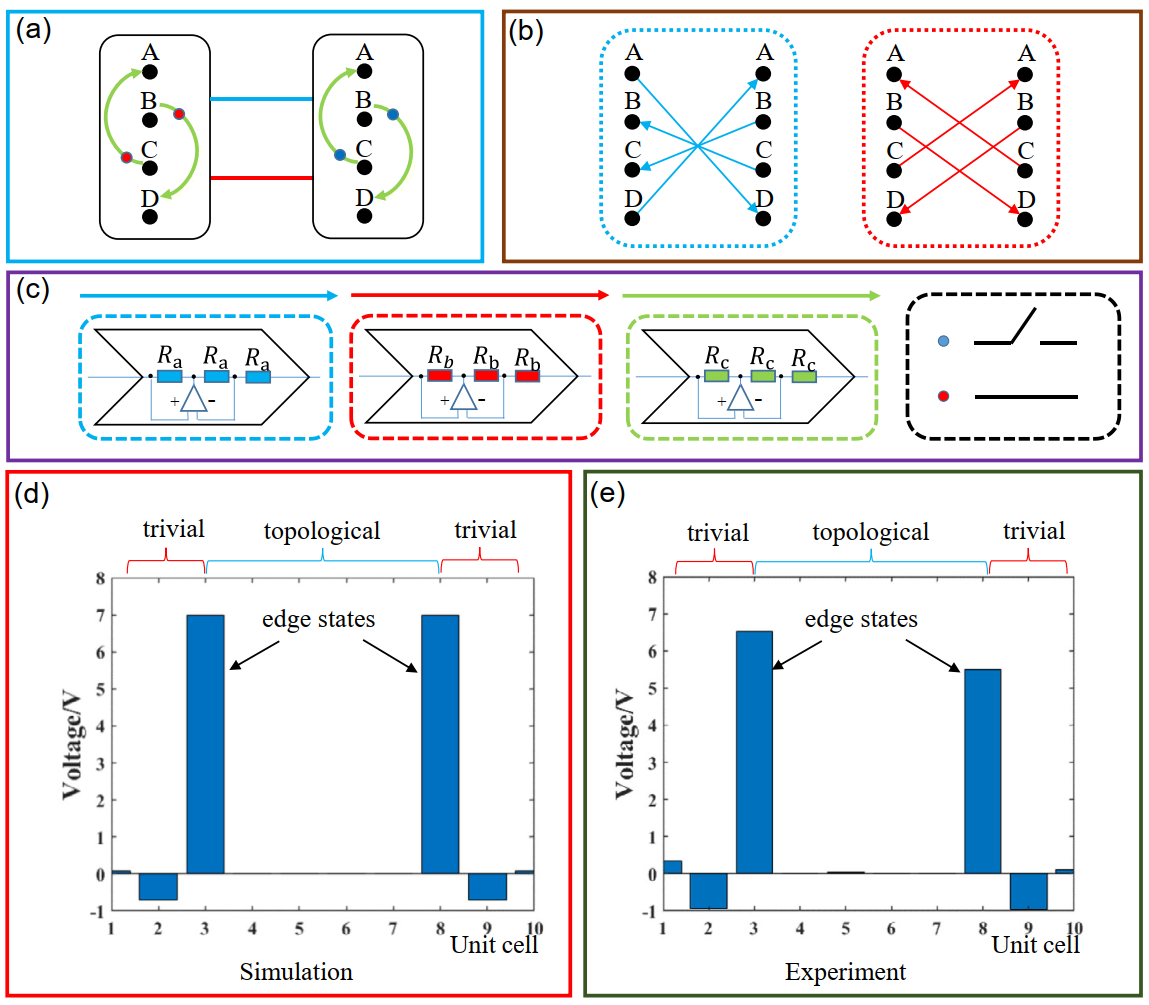
图1. 经典电路构造出类马约拉纳零能模式
当实现了具有粒子空穴对称性的类马约拉纳零能模后，接下来，研究人员通过调控电路中的开关控制零能模的演化轨迹，进而实现编织操作。在实现控制零能模过程中使用了如图2（a）所示的T结。为了实现编织操作，研究人员将零能模的调控分为8步（见图2（c））：
第1步（I到II），通过逐步断开电路节点上的开关，实现缓慢移动3端的零能模到位置2；
第2步（II到III），对于到达位置2的零能模，通过缓慢闭合2至4端的电路节点开关，将位置2的零能模移动到位置4；
第3步（III到IV），此时缓慢断开位置1到2的电路节点开关，实现将位置1的零能模移动到位置2；
第4步（IV到V），通过调节位置2至4处电路上紫色和棕色电阻的大小参数，使得模拟系统的相位从ϕ=0变成ϕ=π；
第5步（V到VI），通过缓慢闭合位置2至3处电路节点的开关，使得位置2处的零能模移动到位置3；
第6步（VI到VII），逐步断开从位置4至2的电路开关，实现将位置4的零能模式缓慢移动至位置2；
第7步（VII到VIII），再次逐步闭合从位置2至位置1的电路开关，实现将位置2的零能模式缓慢移动至位置1；
第8步（VIII到IX），通过调节位置2至4处电路上紫色和棕色电阻的大小参数，使得模拟系统的相位从ϕ=π变成ϕ=0。
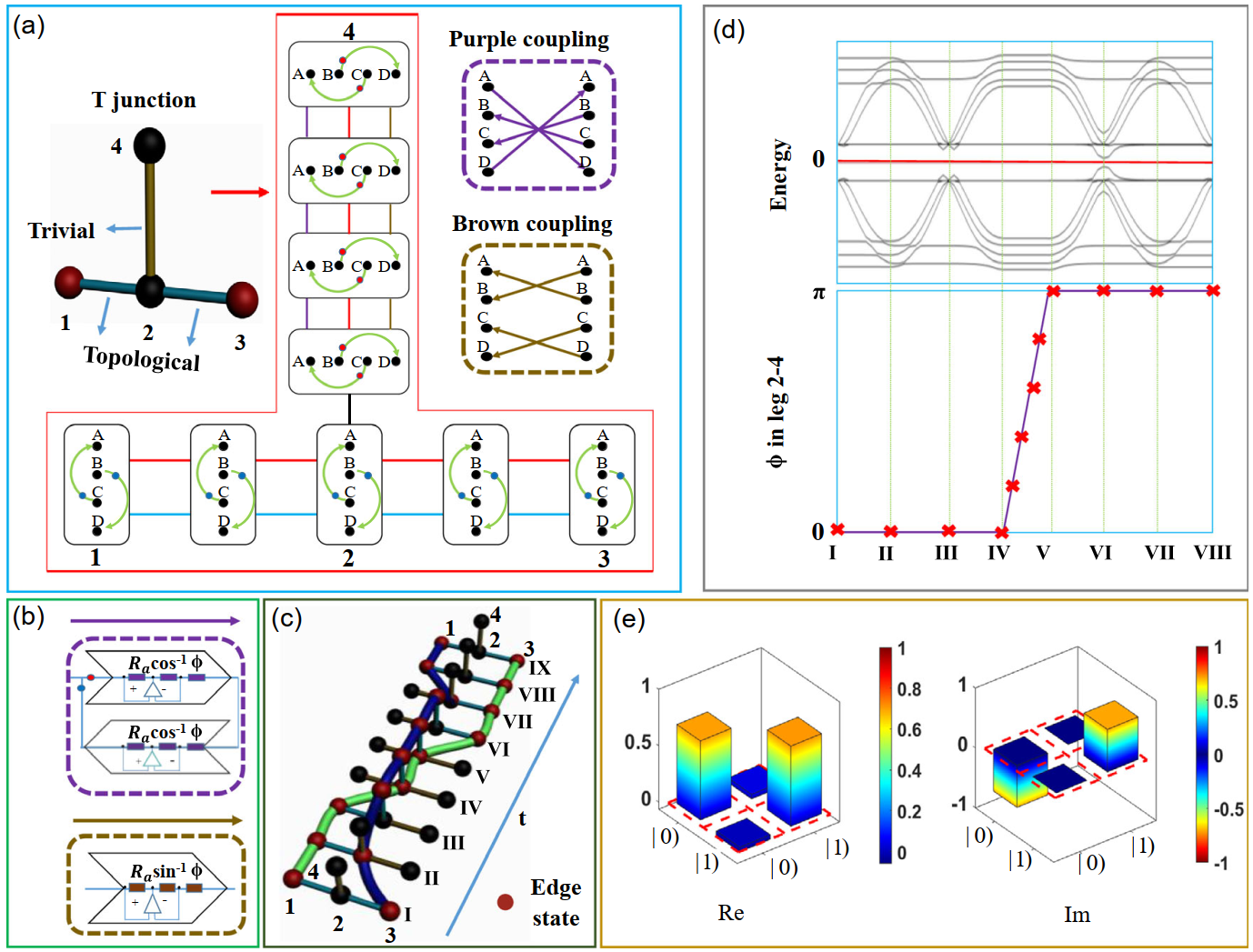
图2. 在经典电路实现编织的功能。
经过上述8个步骤，编织过程完成了V1（0）→V3（0）和 V3（0）→-V1（0）的转化，如图2（c）所示。在编织结束后，研究人员测量1-4每个节点的电压，并通过相应的计算，从而得到了编织矩阵。结果如图2（e）所示，可以清楚地看到输入态|0 ）和|1）成功地被转化为1/ √2（1-i）|0）和1/ √2（1+i）|1） 。通过定量地表征编织过程，研究人员还计算了其保真度F为0.98±0.0069 。这表明编织功能被成功实现了。
研究亮点之二：通过激发多个零能模演示了单比特门和两比特门的功能
为了演示单比特门对应的编织过程，研究人员激发了4个类马约拉纳零能模式。通过控制前3个零能模之间的顺序编织过程，从而实现了单比特Hadamard门所对应的功能，如图3（a）所示；通过控制前2个模式之间的顺序编织过程，从而实现了单比特泡利z门对应的功能，如图3（c）所示。
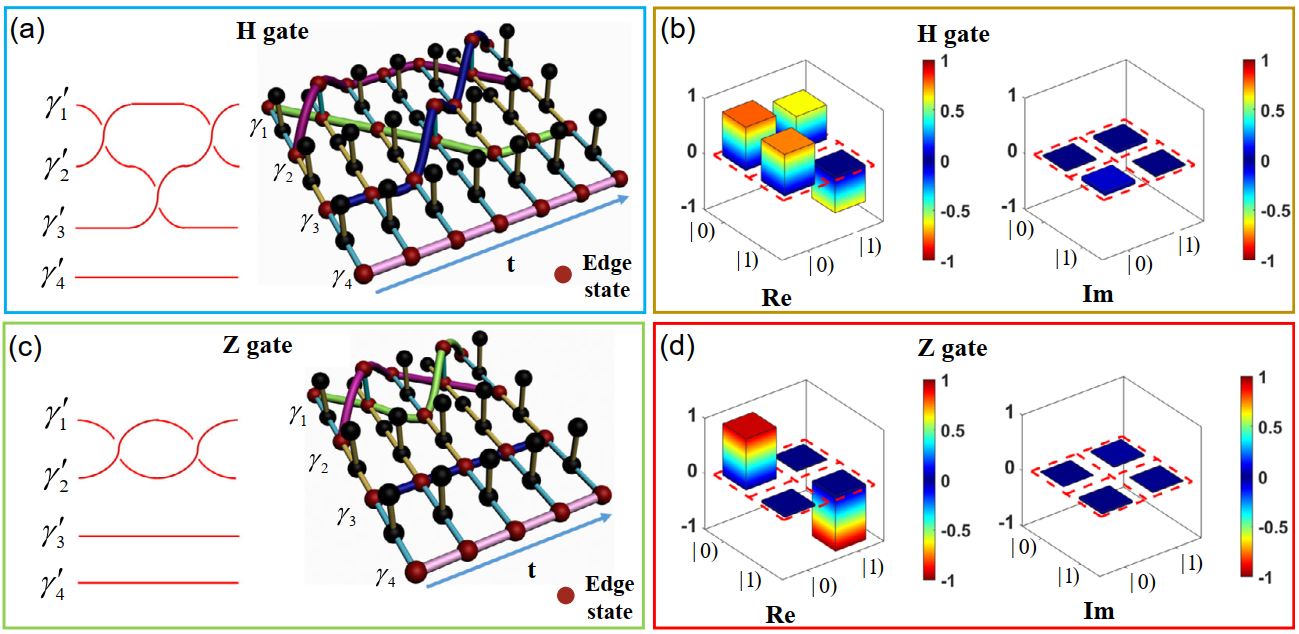
图3. 通过对类马约拉纳零能模式编织实现单比特门。
在具体实验中，基于上述编织过程以及图3（a）和3（c） 中所展示编织顺序，研究人员展示了对应于单比特Hadamard和单比特泡利z门的整个编织过程。通过测量每个节点的电压，并进行相应的计算，得到了对应于单比特Hadamard和单比特泡利z门矩阵，结果如图3（b）和3（d）所示。对于单比特Hadamard门，输入态|0） 和 |1）成功地被转化为|0）+|1） 和|0）-|1） 。通过定量地表征编织过程，计算得到其保真度F=0.9875±0.0083 。对于单比特泡利z门，输入态|0）和|1） 成功地被转化为|0）和-|1） ，其保真度为F=0.9410±0.0102。
不仅仅是可以通过编织零能模式演示单比特门，还可以演示两比特门的功能。如图4所示。研究人员通过激发6个零能模式来实现两种两比特门。通过控制前2个零能模之间的顺序编织，然后控制后4个零能模式的顺序编织过程，从而实现了两比特控制非门（CNOT门）所对应的功能，如图4（a）所示；通过分别控制每两个模式之间的顺序编织过程，从而实现了两比特控制z门（CZ门）对应的功能，如图4（c）所示。
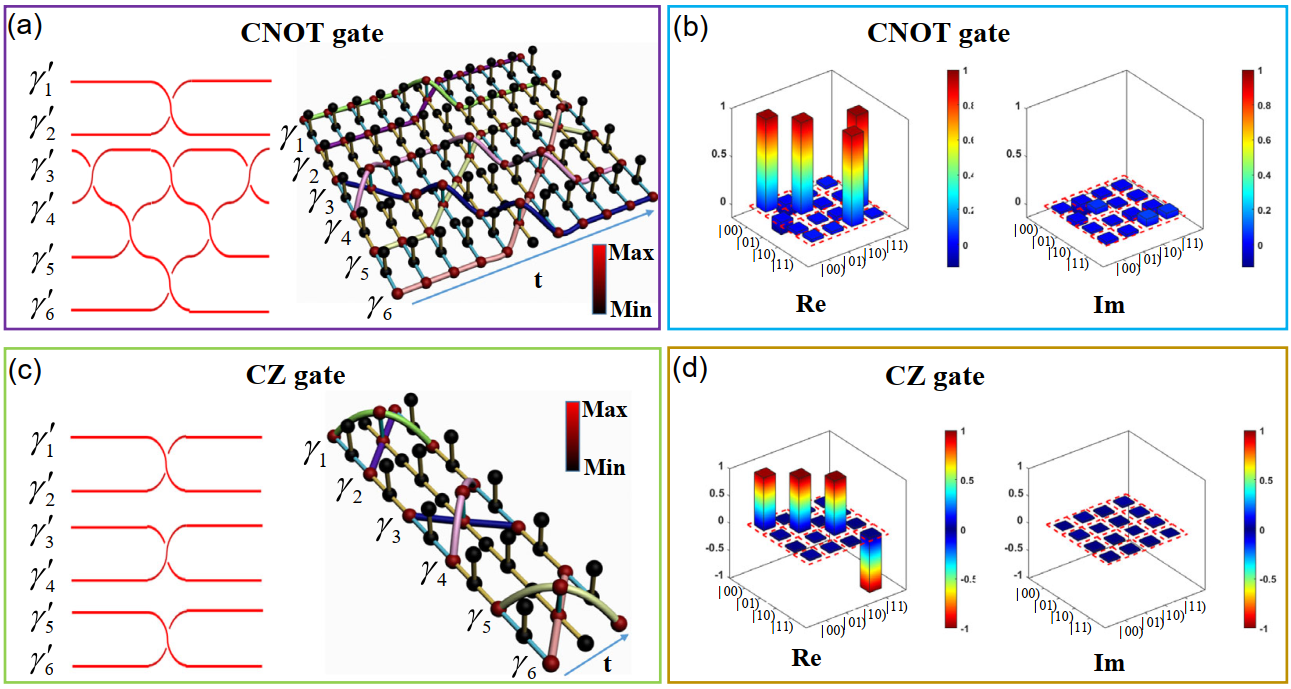图4. 通过对类马约拉纳零能模式编织实现两比特门。
在具体实验中，与单比特门类似，研究人员基于上述编织过程以及图4（a）和4（c）中所展示编织顺序，完成了CNOT门和CZ门的整个编织过程。通过测量每个节点的电压，并进行相应的计算，得到了CNOT门和CZ门矩阵，结果如图4（b）和4（d）所示。对于CNOT门，输入态|00）,|01）, |10）和|11）成功地被转化为 |00）,|01）, |11）和|10）。研究人员计算了其保真度F=0.9098±0.0107。对于CZ门，输入态|00）,|01）, |10）和|11）成功地被转化为|00）,|01）, |10）和-|11）。其保真度为F=0.9409±0.0076。
研究亮点之三：使用多步编织展示了Grover搜索算法的功能
在能够操控零能模展示单比特门和两比特门的基础上，研究人员通过操控更加复杂的零能模编织过程，从而实现Grover搜索算法的功能。如图5（a）和5（b）所示，研究人员通过操控6个零能模式的顺序编织过程，从而演示了两比特Grover搜索的功能。在电路实现中，研究人员使用五个T型结来构建三对（6个）零能模式。通过调节绿色耦合的开关，实现了边缘态的编织功能。按照图5（b）中所展示编织顺序，从而完成了整个搜索过程。
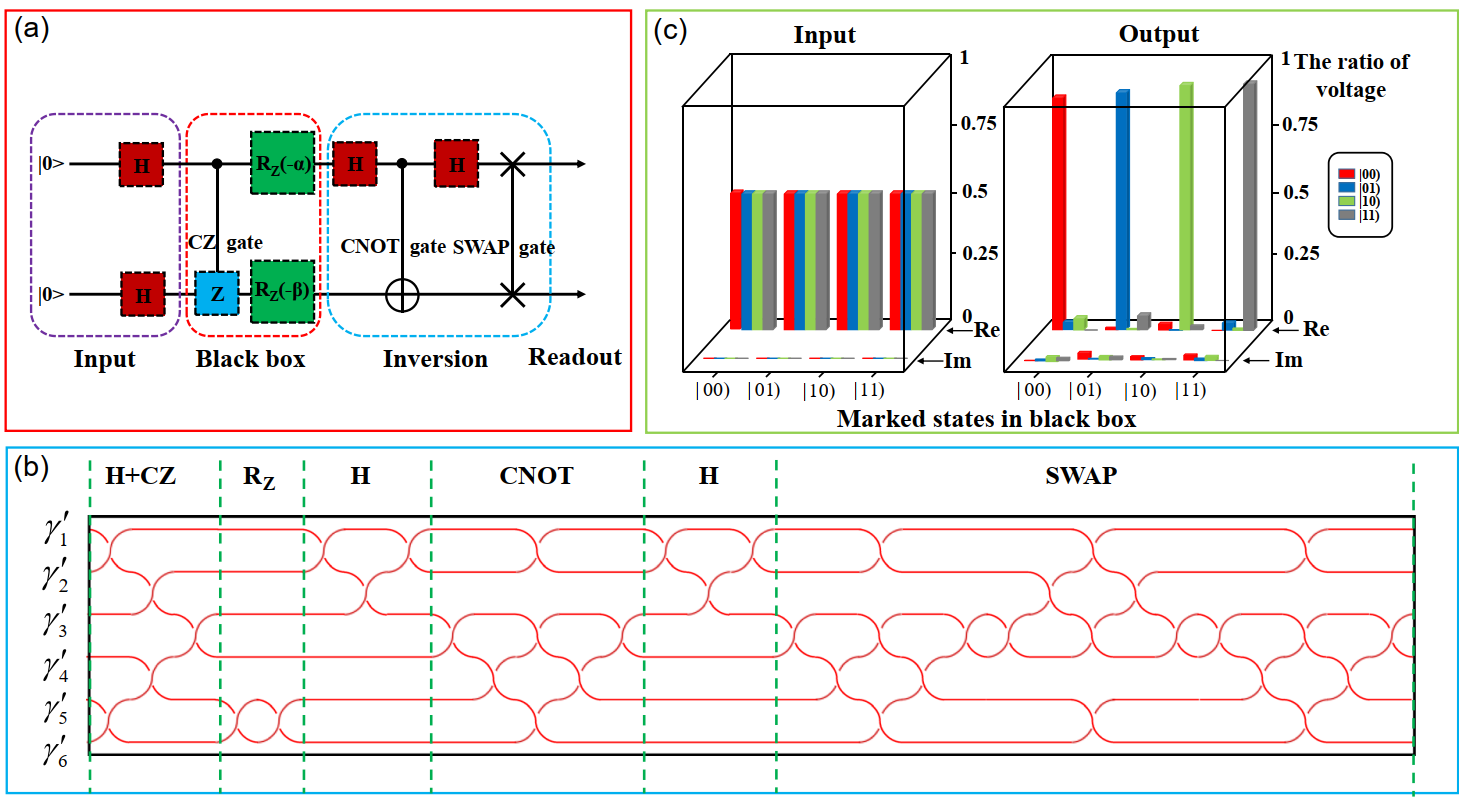
图5. 操控零能模式实现Grover搜索算法功能
研究人员在实验中展示了通过零能模式的编织实现Grover搜索算法的效果。在给定初始输入状态为均匀分布的情况时，在搜索结束后寻找到目标状态的概率都接近于1，见图5（c）。研究人员在实验中考虑了四种不同的目标状态：00，01，10和11。只需要一次检索过程，就能够以极高概率找到目标状态。对于第一种情况，在搜索结束后寻找到目标状态为00的概率为0.93；对于第二种情况，在搜索结束后寻找到目标状态为01的概率为0.93；对于第三种情况，在搜索结束后寻找到目标状态为10的概率为0.96；对于第四种情况，在搜索结束后寻找到目标状态为11的概率为0.95。这表明可以通过设计的编织操作，实现了Grover搜索的功能。
总结与展望
研究人员在实验中利用经典电路构造出具有拓扑保护的类马约拉纳零能模，并且通过操控这些零能模实现了编织功能，也演示了单比特门和两比特门的功能，此外通过使用多步编织展示了Grover搜索算法的功能。这一研究说明如果拓扑量子计算可以使用电路进行模拟，则有望避免现有量子计算方案面临的一些问题，如退相干和可扩展性。此外，电路网络中电阻引起的能量损失也可以通过连接电源来补充。也就是说，所构建的系统能够稳定地工作。因此该工作为构建一个可实用、稳健的快速信息处理系统铺平了道路。