New topological number is defined in nonlinear normal modes of general and strongly nonlinear dynamics
来源: 作者: 发布时间:2022-10-13Topological edge states lead to exotic boundary properties, including robust chiral edge propagations and polarized responses, that are immune to disorders and backscattering. These unconventional states are protected by integer numbers called topological invariants, which cannot be easily changed upon the variation of system parameters unless topological transitions cause these integer numbers to jump. Originally developed in quantum states, this modern concept is extended to classical structures that enable many pioneering applications.
Recently, few efforts address topology in nonlinear systems to uncover novel physics. However, the majority of them focus on Kerr-nonlinear photonic metamaterials, and weakly nonlinear systems that enable Kerr-nonlinear approximations. Kerr-interactions are special nonlinearities that grant sinusoidal nonlinear waves. Consequently, the topological invariants are the same as those in linear theories.
However, most interactions in strongly nonlinear classical system are beyond Kerr-nonlinearities, such as electrical, acoustic, plasmonic, and biophysical systems. As there is no analytic solutions to nonlinear normal modes, the topological invariants are hitherto undefined. Furthermore, strong nonlinearities may destroy the topological nature of weakly nonlinear systems by breaking their intrinsic symmetries or cause instability. Thus, existing linear and weakly nonlinear theories are not always correct to predict topological phases in strongly nonlinear regime. Moreover, it is intriguing to ask what exotic physics arise when topology meets general strong nonlinearities. Thus, it is demanding to invoke the topological number that precisely describes the topological attributes of “beyond-Kerr” general strongly nonlinear dynamics.
In our recent work, we investigate the topological invariant and properties of one-dimensional generalized nonlinear Schrödinger equations. This theoretical framework describes a wide range of nonlinear physics, such as mechanically isostatic frames, electrical circuits, deep water waves, and biophysical processes. As the magnitudes are comparable between the nonlinear and linear parts of the interactions, the system is in the “strongly nonlinear regime”, where perturbation theory naturally breaks down. As a result, nonlinear normal modes are remarkably distinct from sinusoidal waves. Remarkably, this work demonstrates that the notion of adiabatic geometric phase, namely nonlinear Berry phase, can still be derived analytically from these “non-sinusoidal” normal modes.
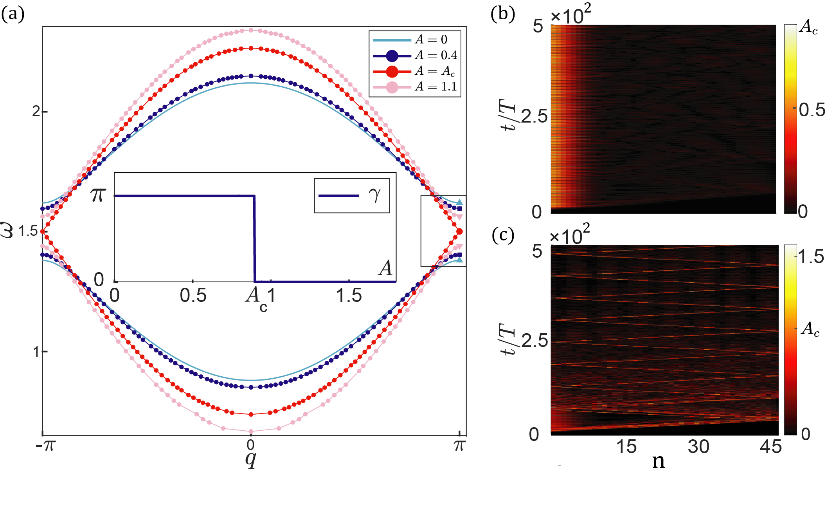
Fig.1. Nonlinear topological bands and boundary normal modes. (a) Amplitude-dependent nonlinear bulk bands. The inset shows the amplitude dependence of quantized nonlinear Berry phase. (b) The spatial-temporal profile of the strongly nonlinear topological normal mode in the topological phase. (c) The absence of nonlinear topological boundary modes in the topologically trivial phase.
Next, without utilizing linear analysis, we establish a symmetry-based non-perturbative strategy, to show the quantization of nonlinear Berry phase under reflection symmetry. The integer-valued nonlinear Berry phase serves as the topological index of the nonlinear system, in which the emergence of nonlinear topological modes corresponds to the non-trivial index. Analogous to the robustness of linear topological states, the topological number protects nonlinear topological modes from disorders.
In summary, our work reveals the universality of the notion of topological protection in strongly and “beyond-Kerr” nonlinear motions. We hope that the geometric Berry phase derived from nonlinear normal modes, and the non-perturbative methodology established in this work, can help trigger future research interests in both topological physics and nonlinear dynamics.
For more information, please refer to our paper published in Nature Communications, “https://www.nature.com/articles/s41467-022-31084-y#citeas”.




